Интересные темы:

Гаджеты

Немного интересного:

Время понимания: сверхпроводимость

10.08.2017 Наука и жизнь

Электроны несут одноименный заряд и исходя из этого не смогут притягиваться друг к другу конкретно. Но при перемещении первый электрон (целая траектория) притягивает положительно заряженные ионы в узлах кристаллической решетки, смещая их и образуя локальный избыток хорошего заряда (и приводя к упругим колебаниям решетки — фононы). Данный заряд притягивает второй электрон (пунктирная линия), связывая две частицы в виртуальную несколько.

Куперовские пары электронов связаны «невидимыми узами» и смогут двигаться лишь согласованно. В случае если один из электронов «натыкается» на недостаток кристаллической решетки (тёмный кружок), он неимеетвозможности рассеяться, потому, что его с громадного расстояния удерживает второй электрон. А отсутствие рассеяния свидетельствует отсутствие электрического сопротивления

Одну из моделей внес предложение британский физик Брайан Пиппард. На протяжении собственных опытов он заключил, что сверхпроводящая территория у поверхности примера распространяется на иную глубину, чем магнитное поле.Время понимания: сверхпроводимость Для описания данной глубины он ввел новый параметр — длину когерентности (ее именуют кроме этого длиной корреляции).

В модели Пиппарда состояние сверхпроводника в конкретной точке зависит от величины магнитного поля не только в ней самой, как у Лондонов, вместе с тем в ее окрестности, масштабы которой определяет протяженность когерентности. Из этого направляться, что в базе сверхпроводимости лежат нелокальные сотрудничества, связывающие пространственно поделённые электроны. В первый раз такую идея высказал в 1935 году Фриц Лондон, а Пиппард выразил ее математически.

Эта мысль была очень плодотворной, но ее физический суть полностью выявился только спустя пара лет.

Вторым обобщением теории Лондонов стала модель, предложенная будущими академиками и нобелелевскими лауреатами Виталием Львом и Гинзбургом Ландау. Она основана на феноменологической теории фазовых переходов второго рода, сформулированной Ландау во второй половине 30-ых годов XX века. Эта теория актуальна и сейчас — действительно, в пара откорректированном виде.

Ландау осознал, что фазовый переход второго рода является изменениемвнутренней симметрии (либо, что то же самое, степени внутренней упорядоченности) физической совокупности. К примеру, в случае если нагреть ферромагнетик до температуры Кюри, ядерные магнитные моменты лишатся прошлой параллельной ориентации — это и имеется фазовый переход второго рода. Ландау внес предложение для описания таких переходов особенную величину- параметр порядка (для ферромагнетиков это магнитный момент единицы количества).

В соответствии с его теории, в фазе с меньшей упорядоченностью среднее значение параметра порядка равняется нулю, а в более упорядоченной фазе превосходно от нуля и по мере повышения степени упорядоченности возрастает по полной величине.

Гинзбург и Ландау трактовали происхождение сверхпроводящего состояния в отсутствие магнитного поля как фазовый переход второго рода. В качестве параметра порядка они ввели комплексную функцию, квадрат модуля которой пропорционален плотности носителей сверхпроводящего тока. При температурах выше критической эта плотность равна нулю, при более низких возрастает и достигает максимума при безотносительном нуле.

Гинзбург и Ландау написали совокупность из двух уравнений, связывающих параметр порядка с плотностью электрического тока и магнитным полем. Эти уравнения не растолковывают обстоятельств сверхпроводимости, но прекрасно обрисовывают поведение сверхпроводника вблизи критической температуры. В модели Гинзбурга и Ландау фигурирует заряд носителей сверхпроводящего тока, что эта теория не определяет.

Ландау полагал его равным заряду электрона, Гинзбург в этом сомневался, но до поры до времени вопрос остался открытым.

Вихри Абрикосова

При ответе уравнений Гинзбурга-Ландау появляются две величины, имеющие размерность длины. Первая — это лондоновская глубина проникновения магнитного поля, вторая же фактически сходится с пиппардовской длиной корреляции. Оказалось, что свойства сверхпроводника значительным образом зависят от параметра, примерно равного отношению этих размеров при нулевой температуре.

В случае если данный параметр меньше приблизительно 0,7, сверхпроводник ведет себя в магнитном поле как совершенный диамагнетик и всецело подчиняется эффекту Мейсснера-Оксенфельда. В другом случае появляются осложнения, физический суть которых тогда не был понятен. Но Гинзбург и Ландау сделали вывод, что таковой режим не следует разглядывать, потому, что практически данный параметр неизменно большое количество меньше единицы.

Действительно, к тому времени экспериментаторы уже узнали, что это вовсе не обязательно, но до Гинзбурга с Ландау эти сведения еще не дошли.

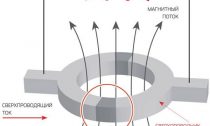
Следующий ход сделал сотрудник Ландау по теоретическому отделу Университета физических неприятностей Алексей Абрикосов. Он продемонстрировал, что разглядывать второй вариант все-таки стоит, потому, что в этом случае сверхпроводник может снизить внутреннюю энергию, пропустив вглубь внешнее магнитное поле. Для этого нужно, дабы напряженность поля превысила нижнее критическое значение Hc1, определенное группой Шубникова (см. «ПМ» №8’2011).

Абрикосов выделил такие сверхпроводники в особенное семейство и назвал их сверхпроводниками второй группы (либо, как говорят на данный момент, второго рода). Из его уравнений направляться, что внешнее магнитное поле попадает в сверхпроводник второго рода в виде нитей, каковые именуют вихрями Абрикосова. Любой вихрь несет единственный квант магнитного потока, предсказанный еще Фрицем Лондоном.

Сердцевина вихря является трубкойрадиусом порядка длины когерентности, и вещество в ней находится не в сверхпроводящем, а в обычном состоянии. Трубку охватывают вихревые токи, текущие в слоя толщиной приблизительно с лондоновскую глубину проникновения, каковые экранируют от магнитного поля сверхпроводящие территории между вихрями. В следствии появляется смешанное состояние (также термин Абрикосова), в котором сверхпроводник пронизан вкраплениями обычной фазы.

Плотность вихрей возрастает по мере нарастания магнитного поля. Если оно только мало превосходит Hc1, вихри выстраиваются на большом растоянии друг от друга и практически не взаимодействуют между собой. При повышении поля токи соседних вихрей перекрываются, и между вихрями появляются силы отталкивания. Вследствие этого вихри формируют что-то наподобие кристаллической решетки, которая в однородных сверхпроводниках складывается из треугольных ячеек.

При возрастании поля ячейки стягиваются, и по достижении Нс2 обычные сердцевины соседних вихрей сливаются между собой. Объемная сверхпроводимость разрушается, и внешнее магнитное поле всецело попадает вовнутрь примера. Так, теория Абрикосова растолковала результаты экспериментов харьковских физиков.

А смешанное состояние сверхпроводника второго рода часто именуют шубниковской фазой.

Как поведал «Популярной механике» сам Алексей Абрикосов, что на данный момент трудится в Соединенных Штатах в Аргоннской национальной лаборатории, Ландау продолжительно не признавал его выводов, потому, что происхождение вихрей не стыковалось с теорией Лондонов: «То, что лондоновские уравнения теряют силу в масштабах межатомных расстояний, было осознано не сходу». Опыты подтвердили выводы Абрикосова только в середине 1960-х, а в 2003 году он в один момент с Виталием Гинзбургом был удостоен Нобелевской премии.

Сверхпроводимость на три буквы

В первой половине 50-ых годов двадцатого века, практически в один момент с возникновением моделей Пиппарда и Гинзбурга-Ландау, американские физики-экспериментаторы Чарльз Бернард и Рейнольдс их соотечественник и Серин Эммануэль Максвелл поняли, что у изотопов ртути критическая температура перехода в сверхпроводящее состояние изменяется обратно пропорционально квадратному корню из ядерного веса. Это прямо показывало, что сверхпроводимость появляется при участии колебаний кристаллической решетки, частота которых подчиняется такой же зависимости.

Незадолго до этого к такому же выводу пришел и доктор наук теоретической физики Ливерпульского университета Герберт Фрёлих. Модель Фрёлиха не растолковала результата Мейсснера-Оксенфельда, но подкрепила подозрения, что сверхпроводящее состояние появляется на стыке между электронами и атомами.

Тогда же сверхпроводимостью занялся и Джон Бардин, один из создателей транзистора. Он вспоминал о ней еще в предвоенные годы, а по окончании открытия изотопического результата возвратился к данной проблеме. В первой половине 50-ых годов XX века в Университете Иллинойса Бардин действительно занялся сверхпроводимостью.

Его первая модель, созданная совместно с Дэвидом Пайнсом, была не через чур успешной, но все же учитывала сотрудничество между колебаниями и электронами кристаллической решетки. В 1955 году Бардин привлек себе в помощь блестящих молодых теоретиков Леона Роберта и Купера Шриффера. Результатом сотрудничества стала страно прекрасная модель, вошедшая в историю физики как БКШ-теория (по первым буквам фамилий).

Начало ей положил Леон Купер. Во второй половине 50-ых годов двадцатого века он теоретически продемонстрировал, что вблизи безотносительного нуля электроны проводимости в металле в принципе способны вырабатывать пары, объединяющие частицы с равными и противоположно направленными импульсами. Для этого необходимо, дабы между электронами существовало притяжение, пускай сколь угодно не сильный.

Потому, что в следствии спаривания полная энергия совокупности значительно уменьшается, такое состояние владеет определенным запасом прочности и само по себе не разрушается.

Но откуда взяться притяжению, коль не так долго осталось ждать электроны отталкиваются по закону Кулона? Как додумался еще Фрёлих, его может создать кристаллическая решетка, складывающаяся из хороших ионов. Потому, что движущийся электрон притягивает близлежащие ионы, они смещаются в его сторону и создают локальный избыток хорошего заряда. Поляризованный участок решетки, со своей стороны, может притянуть второй электрон, что сдвинется по направлению к первому.

Само собой разумеется, для этого нужно, дабы опосредованное решеткой притяжение электронов преобладало над кулоновским отталкиванием. Это растолковывает, из-за чего лучшие проводники, такие как медь и серебро, не преобразовываются в сверхпроводники: их электроны проводимости через чур слабо взаимодействуют с ионами решетки.

В теории жёсткого тела упругие колебания кристаллической решетки описываются как перемещение фононов — квантов звуковых волн. В этих терминах спаривание электронов появляется благодаря обмену фононами, либо, как говорят физики, электрон-фононному сотрудничеству. Возможно заявить, что электроны притягиваются, испуская и поглощая фононы.

Этот механизм заложен в базу теории БКШ. Но исходная модель Купера имеет более характер, потому, что говорит о возможности спаривания электронов под действием любого действенного притяжения, вовсе не обязательно обусловленного обменом фононами. Такие другие механизмы сверхпроводимости, по всей видимости, существуют, но их действительность еще совсем не доказана.

Обычное электрическое сопротивление появляется из-за рассеивания носителей тока на тепловых колебаниях решетки (в противном случае говоря, фононах), и на иных неоднородностях и атомах примесей. В случае если ток переносят отдельные электроны, то сопротивление не может быть нулевым, потому, что они рассеиваются при любых энергиях. Иное дело, в случае если в этом качестве выступают куперовские пары (несущие, конечно, двойной электронный заряд).

Спаренный электрон может претерпеть рассеяние, лишь порвав сообщение с партнером. Исходя из этого для разрушения сверхпроводимости средняя скорость, которую набирают электроны во внешнем электрическом поле, обязана превышать определенный предел, пропорциональный энергии связи электронных пар. Эта предельная скорость соответствует критической плотности тока.

Парные связи должны разрываться и при сотрудничестве с фононами высоких энергий, что и происходит при увеличении температуры выше критической. Ниже данной границы куперовские пары при встрече с фононами значительно чаще не рвутся, а просто переходят в новые состояния.

Теория БКШ растолковывает и эффект Мейсснера. Потому, что спаренные электроны движутся с противоположными импульсами, в магнитном поле на них действуют силы, направленные в различные стороны и потому трудящиеся на разрыв пары. В случае если напряженность поля мала, сверхпроводнику удачнее вытолкнуть его на поверхность и удержать куперовские пары в связанном состоянии. Не смотря на то, что такое выталкивание требует расхода энергии, он с лихвой компенсируется ее экономией при сохранении куперовских пар.

Теория БКШ кроме этого разрешает осознать физический суть длины когерентности, которая соответствует средней расстоянии между спаренными электронами. Эта протяженность приблизительно равна 10−5 см и потому в тысячи раз превышает межатомные расстояния.

Во второй половине 50-ых годов XX века издание Physical Review опубликовал маленькое письмо Бардина, Купера и Шриффера «Микроскопическая теория сверхпроводимости», за которым скоро последовала 20-страничная статья «Теория сверхпроводимости». Эти две работы растолковывали, из-за чего и как вещество преобразовывается в сверхпроводник. Примечательно, что в том же году в ЖЭТФ показалась и статья Абрикосова «О магнитных особенностях сверхпроводников второй группы».

Затишье перед бурей

Во второй половине 50-ых годов двадцатого века сотрудник Абрикосова Лев Горьков продемонстрировал, что вблизи критической температуры уравнения Гинзбурга-Ландау являются следствием теории БКШ. А в первой половине 70-ых годов двадцатого века микроскопическая теория сверхпроводимости принесла своим авторам Нобелевскую премию.

Но эта теория имеет важное ограничение — она не разрешает угадать свойства новых сверхпроводников. Американский физик Бернд Маттиас, в 1950—1970-х годах открывший много сверхпроводящих материалов, остроумно увидел, что теория БКШ «растолковывает все, но не разрешает отыскать ничего». Но, нет правил без исключений.

В первой половине 60-ых годов двадцатого века на базе теории БКШ был сделан необычный прогноз, скоро подтвержденный в опыте. Все куперовские пары движутся как единое целое и потому описываются единой волновой функцией. В силу квантового туннельного результата эта функция способна «просочиться» через энергетический барьер. В этом случае барьером возможно узкий слой диэлектрика, разделяющий два сверхпроводника.

Первую действующую схему со сверхпроводящим туннельным контактом собрал сотрудник исследовательской лаборатории корпорации General Electric Айвар Джайевер в первой половине 60-ых годов двадцатого века. Но настоящий прорыв был достигнут два года спустя, в то время, когда британский физик Брайан Джозефсон теоретически продемонстрировал, что через диэлектрик туннелируют сверхпроводящие токи, каковые владеют неповторимыми особенностями чисто квантовой природы.

За открытие этого результата Джозефсон (вместе с Джайевером и Лео Эсаки) в первой половине 70-ых годов XX века взял Нобелевскую премию. на данный момент данный эффект активно используется — в частности, на его базе трудятся сквиды, сверхчувствительные сверхпроводящие магнитометры.

вихри и Фазовые переходы

Фазовые переходы I и II рода — это, например, кипение и таяние льда воды. При аналогичных переходах выделяется либо поглощается тепло, плотность изменяется скачками, теплоемкость делается нескончаемой. Тотальное разрушение сверхпроводимости магнитным полем — это именно и имеется фазовый переход I рода.

Хорошие примеры фазовых переходов II рода- превращение парамагнетика в ферромагнетик либо в антиферромагнетик. Плотность в этих обстоятельствах изменяется непрерывно, теплота не выделяется и не поглощается, теплоемкость изменяется скачком, но не обращается в бесконечность.

Вихри в сверхпроводнике II рода возможно представить как «виртуальные» соленоиды, образованные сверхпроводящими круговыми токами, ось которых параллельна внешнему магнитному полю. Вне вихрей магнитное поле равняется нулю.

Пришпилить вихри

Происхождение смешанной фазы определяет реакцию сверхпроводника II рода на прохождение электрического тока от внешнего источника.

В случае если сила тока мала и созданное им магнитное поле меньше Hc1, абрикосовских вихрей не появляется. В то время, когда поле транспортного тока преступает эту границу, вихри рождаются у поверхности и мигрируют вглубь. В случае если электроны рассеиваются на обычных сердцевинах вихрей, пример обретает электрическое сопротивление. Дабы этого не случилось, вихри необходимо остановить, цепляя их к намерено созданным неоднородностям кристаллической решетки.

Именно поэтому через сверхпроводники II рода удается пропускать токи, плотность которых достигает миллионов ампер на 1 см?.

чтение мыслей и Слабое звено

Электроны (правильнее, куперовские пары) в сверхпроводнике движутся как единое целое, причем их количество неимеетвозможности быстро изменяться в окрестностях, меньших длины когерентности, которая намного больше межатомных расстояний. А это указывает, что состояние сверхпроводимости как бы «выходит» за пределы границы сверхпроводника (в случае если ему не мешает магнитное поле) и распространяется (в пределах длины когерентности) на соседние области.

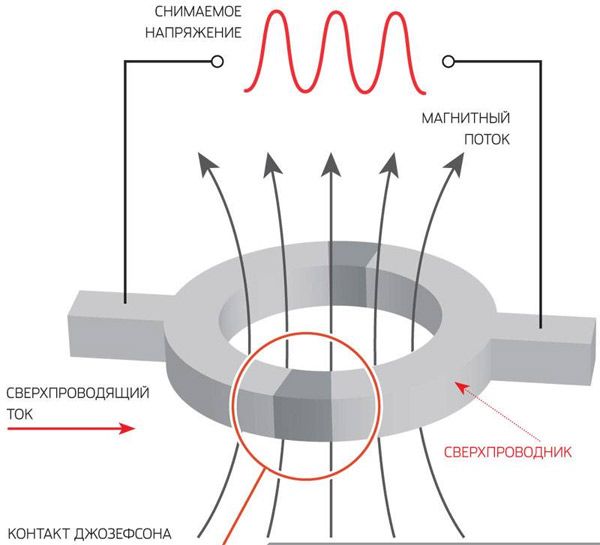
Исходя из этого, в случае если поделить два сверхпроводника диэлектриком меньшей толщины, мы возьмём так называемый контакт Джозефсона, именуемый кроме этого не сильный звеном сверхпроводящей цепи. Электроны туннелируют через таковой барьер, и через контакт течет сверхпроводящий ток. Потому, что по различные стороны контакта куперовские пары движутся в разных фазах, ток через не сильный звено определяется их разностью, другими словами интерференцией волновых функций.

На базе результата Джозефсона выстроены самые чувствительные устройства для измерения магнитного поля — сверхпроводящие квантовые интерференционные устройства, сквиды (от англ. superconducting quantum interference device, SQUID). Один из вариантов конструкции сквидов представляет собой петлю из сверхпроводника с двумя не сильный звеньями, через каковые течет постоянный ток.

Изменение магнитного потока через петлю сквида порождает в ней кольцевой ток, что изменяет баланс токов между не сильный звеньями. Наряду с этим со сквида возможно снимать напряжение, зависящее от трансформации магнитного потока. На иллюстрации продемонстрировано изменение напряжения при возрастании магнитного поля, причем каждому периоду соответствует изменение на единичный квант магнитного потока.

Чувствительность сквидов довольно большая — они разрешают обнаруживать трансформации магнитного поля менее чем в 10−14 тесла. Один из самые известных примеров применения сквидов — магнитоэнцефалография, регистрация весьма не сильный магнитных полей (порядка 10−13 тесла), появляющихся в ходе электрической активности мозга.

Статья размещена в издании «Популярная механика» (№107, сентябрь 2011).

Случайные записи:

Михаил Малахов — Что такое сверхпроводимость?


Похожие статьи, которые вам понравятся:

Tags:  , ,