Парадокс легкой модели

«Самая заветная мечта — высота, высота…» Так поется в известной песне о летчиках. Высота — заветная мечта и моделистов-ракетчиков, в каком бы классе соревнований ни выступал спортсмен. Для «высотных» моделей это прямая цель, а планирующим и парашютирующим собранная высота гарантирует хорошую длительность полета.

Спросите любого моделиста, что необходимо сделать, дабы модель поднялась на громаднейшую высоту, и в числе многих верных ответов — уменьшить аэродинамическое сопротивление, поставить двигатель с большей удельной тягой, обеспечить хорошую стабилизацию полета — и других точно будет и таковой: «Сделать модель как возможно легче». Казалось бы, верно, но в действительности весьма легкая модель может летать так же не хорошо, как и относительно тяжелая.

Назовем это занимательное явление «парадоксом легкой модели» и давайте разберемся в его обстоятельствах.

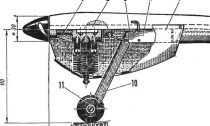
Модель ракеты относится к классу неуправляемых баллистических ракет. Траектория их полета складывается из двух главных участков: активного, на котором трудятся двигатели, и пассивного, на котором ракета летит подобно камню, кинутому старой метательной машиной — баллистой. 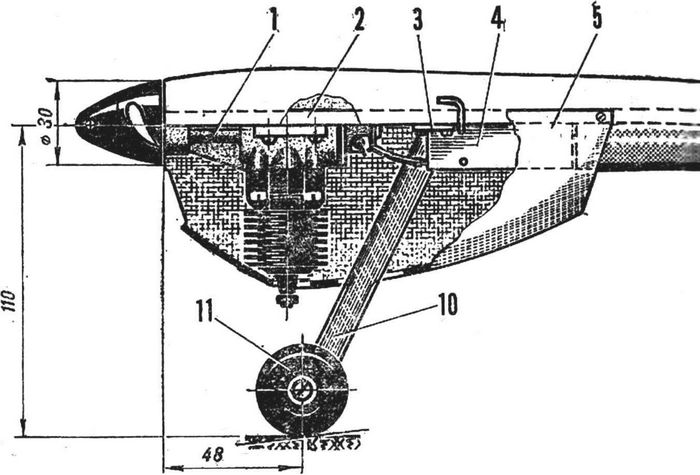Траекторное перемещение ракеты результат действия на нее различных сил.

Какие конкретно же силы действуют на ракету в полете!

Обратимся к авторитету, которому самому довелось испытать эти силы. Послушаем, как отвечает на вопрос о том, с какими силами приходится иметь дело ракете, второй коммунистический посланник в космос — Герман Степанович Титов:

«Во-первых, с тягой двигателя, во-вторых, с силой сопротивления воздуха и, наконец, с весом ракеты.

Между этими сипами, образно говоря, идет борьба: тяга двигателя влечет ракету вперед, сопротивление воздуха мешает ее перемещению, а вес ракеты тянет вниз. В полете величины этих сил изменяются. Изменяется и направление их действия».

От того, какие конкретно силы будут иметь перевес, зависит перемещение ракеты и ее конечный итог — траектория полета.

Силы, действующие на ракету, на активном и пассивном участках разны. В первом случае на вертикально взлетающую модель действует сила тяги двигателей, направленная вверх и разгоняющая ее, и аэродинамического сопротивления и силы тяжести, тормозящие перемещение ракеты и направленные вниз. Во втором — остаются лишь две тяжести: и силы сопротивления.

Самый сложен при анализе полета деятельный участок траектории: на нем изменяются не только силы, но и масса ракеты. Производя горючее, многие современные ракеты изменяют собственную массу многократно.

Изменение массы ракеты в ходе ее перемещения не разрешает применять конкретно те формулы, каковые взяты в хорошей механике Ньютона.

В самый полном и строгом виде подход к изучению перемещения тел переменной массы был в первый раз рассмотрен русским

механиком И. В. Мещерским. В собственной магистерской диссертации «Динамика точки переменной массы», написанной во второй половине 90-ых годов XIX века, он взял строгие уравнения перемещения тела переменной массы при разных догадках отбрасывания весов. Независимо от Мещерского применительно к ракетам изучил перемещение тела переменной массы К. Э. Циолковский.

Теорию перемещения ракеты сейчас именуют ракетодинамикой, а Циолковского по праву вычисляют основоположником современной ракетодинамики.

Думая о тайнах полета ракеты, Циолковский шел глубоко научным методом, последовательно вводя главные силы, от которых зависит перемещение ракеты. Дабы узнать возможности самого реактивного принципа перемещения тел, ученый разглядел несложную задачу-предположение: полет ракеты, на которую действует лишь сила тяги.

Эта задача на данный момент именуется первой задачей Циолковского. Один из ее наиболее значимых выводов гласит, что для одноступенчатой ранеты скорость в конце активного участка будет тем больше, чем больше отношение весов в начале и в конце полета.

Графический способ определения высоты полета.

Во второй задаче Циолковский разглядел вертикальный подъем ракеты с Почвы, лишенной воздуха.

Анализ продемонстрировал, что высота активного подъема ракеты также будет расти при повышении отношения ее начальной массы и конечной.

Настоящий полет ракеты в воздушной среде усложняет задачу так, что взять ответ в виде несложных формул не удается, и достаточно совершенно верно рассчитывать перемещение ракеты под действием всех трех сил обучились недавно, применяя «счеты XX века» — электронные счётные автомобили.

Но как следует выводы первой и второй задач Циолковского остаются честными для вертикального подъема ракеты либо модели в воздухе: с ростом отношения начальной и конечной весов возрастают как скорость, так и высота в конце активного участка траектории.

Для иллюстрации приведем результаты расчета высоты подъема моделей, имеющих различные веса при старте (см. рис.).

Траектория полета рассчитывалась методом решения сложных дифференциальных уравнений на электронной счётной машине. Для расчета была забрана одноступенчатая модель с диаметром мидельного сечения 22 мм и коэффициентом лобового сопротивления 0,75. Двигатель модели имеет полный импульс 10 Н·с и формирует реактивную силу 5 Н в течение двух секунд. Масса горючего в двигателе образовывает 20 г. Начальную массу при расчете изменяли, дабы сравнить высоту подъема моделей.

График А показывает высоту активного полета. При повышении начальной массы ракеты и постоянной мессе горючего отношение начальной и конечной весов значительно уменьшается. Так, для начальной массы 40 г это отношение равняется 2, а для 100 г —1,25.

Соответственно высота активного подъема в первом случае образовывает 200 м, а во втором — 85 м, а скорости в конце активного участка — 160 м/сек и 84 м/сек.

Так, облегчение модели ведет к повышению высоты активного полета, и громаднейшей эта высота станет, в случае если вся ракета будет складываться из одного топлива, другими словами иметь массу на старте 20 г. Само собой разумеется, данный вариант нереален, но он воображает интерес как предельный случай самой легкой модели.

По графику для таковой сверхлегкой модели высота активного подъема достигает 245 м.

Предельным случаем сверхтяжелой модели, в то время, когда ракета по большому счету не сможет взлететь, есть вариант, при котором конечный вес модели будет больше тяги двигателя. Расчетная модель, к примеру, не взлетит при начальной массе более 500 г.

Обратимся сейчас к пассивному участку траектории (график Б].

Как воздействует на высоту баллистического полета облегчение либо утяжеление модели? На этом месте масса ракеты постоянна и равна конечной (начальной массе без горючего). Тут возможно воспользоваться вторым законом Ньютона, которым гласит, что ускорение тела пропорционально силе, действующей, на него пропорционально массе.

Разумеется, что подъем ракеты на пассивном участке будет тем выше, чем меньшее ускорение испытывает она под действием воздушного сопротивления и сил тяжести. Ускорение гравитационных сил в пределах высот подъема моделей можно считать постоянным. При одном и том же сопротивлении ракета, имеющая громадную массу, будет испытывать меньшее ускорение и поднимется на громадную высоту.

Итак, более тяжелая ракета при постоянной скорости в конце активного участка имеет более протяженный участок пассивного подъема. Но необходимо учитывать, что с утяжелением ракеты конечная скорость ев активного полета понижается. Под действием этих двух факторов высота пассивного подъема с ростом начальной массы сперва возрастает, а после этого значительно уменьшается.

Для расчетной модели высота пассивного подъема станет громаднейшей при стартовой массе, равной 65 г.

Весьма интересно подчернуть, что «сверхлегкая» модель совсем не имеет пассивного участка. Не забывайте тайную? «Что может поднять младенец, а силач и через ручей не перебросит?» Ответ: «Пушинку». Вправду, попытайтесь кинуть пушинку: на большом растоянии она не полетит, как бы очень сильно ее ни бросали.

Так и для модели. В случае если выполнить ее через чур легкой, высоко она не встанет, какую бы скорость ей ни информировали в конце активного участка.

Значит, облегчая модель, мы фактически лишаем ее возможности пассивного полета, утяжеляя — ухудшаем условия и итог (высоту и конечную скорость) активного полета. Между этими двумя крайними случаями где-то находится «золотая середина» модель, владеющая оптимальной начальной массой.

Эту массу возможно выяснить для расчетной модели по графику В, где представлена суммарная высота активного и пассивного участков полета. Она образовывает 53 г, а высота ее подъема равна 395 м. Более легкие и более тяжелые модели имеют меньшую высоту. Однообразные высоты возможно взять и для легких, и для тяжелых ракет. К примеру, высоту 345 м возможно взять для моделей с начальными весами 30 г и 90 г.

Итак, явление «парадокса легкой модели» приводит нас к выводу, что не всегда необходимо стремиться облегчать модель: уменьшение массы модели сверх оптимального значения не дает выигрыша в высоте. Поиски оптимального значения стартовой массы собственной модели — одна из задач ракетомоделиста, ответ которой разрешит добиться ему отличных показателей в соревнованиях.

В.

КАНАЕВ, инженер

Случайные записи:

• Таймерная модель «лебедь ов-02»
• Планер f1-a

Fermi Paradox Great Filters: Rare Intelligence

Похожие статьи, которые вам понравятся:

• Силовые установки моделей кораблей

  БАЗЫ ПРОЕКТИРОВАНИЯ. Как мы знаем, любая самоходная модель, будь то модель самолета, корабля либо автомобиля, имеется машина, и, значит, существующие для…

• Гоночная модель «бесхвостка»

  Спортивные результаты в классе гоночных кордовых моделей значительно растут из года в год. Возможно выделить три главных направления, в которых трудятся…

• «Старейшая» категория ракетных моделей

  Из всех классов и видов ракетных парашютных моделей категория S3 самая «старая». На развития и заря возникновения ракетомоделизма одним из параметров…

• Модель опирается на воздух

  Крылья, подобные авиационным, в далеком прошлом уже показались на автомобиле. Сперва это были треугольные плоскости, похожие на плавники рыб. По плану…